Teorema del guscio sferico

Nella meccanica classica, il teorema del guscio sferico (o semplicemente teorema del guscio) consente di semplificare lo studio della gravitazione in presenza di corpi con simmetria sferica.

Formulato da Isaac Newton, che elaborò la teoria della gravitazione universale, esso si compone di due affermazioni:

1. un guscio sferico di massa M, avente densità uniforme, esercita su una particella esterna una forza gravitazionale pari a quella di una particella puntiforme di massa M posta nel suo centro;
2. la forza gravitazionale esercitata da un guscio sferico avente densità uniforme su una particella posta al suo interno è nulla.

Le dimostrazioni originali di Newton fanno uso della geometria e di qualche passaggio al limite, e si trovano rispettivamente alle proposizioni 71 e 70 del libro primo dei suoi Principia. In tempi più recenti, lo stesso teorema viene dimostrato facendo ricorso all'analisi (vedi in seguito).

Il teorema, pur essendo stato sviluppato per la forza gravitazionale, si applica anche alla forza elettrostatica e a qualsiasi fenomeno in cui la forza dipende dall'inverso del quadrato della distanza.

Dimostrazione

Prima affermazione

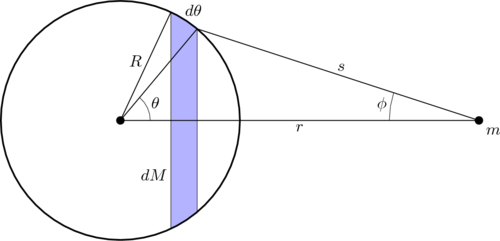
Consideriamo un guscio sferico di raggio R e spessore infinitesimo e una particella di massa m posta a distanza $r$ dal centro del guscio. Possiamo considerare il guscio come costituito da una serie di anelli di raggio $R\sin \theta$, spessore $Rd\theta$ e massa $dM$, con $0\leq \theta \leq \pi$ (la figura a lato ne mostra una sezione trasversale).

Per la legge della Gravitazione, la forza di attrazione esercitata da ciascuno di questi anelli è

$dF={\frac {Gm\;dM}{s^{2}}}\cos \phi$

ed è diretta lungo $r$, in quanto per la simmetria dell'anello le componenti della forza perpendicolari ad $r$ si annullano.

La forza totale esercitata dal guscio è data da:

$F=\int dF=Gm\int {\frac {dM\cos \phi }{s^{2}}}$

occorre ora esprimere $dM$ e $\cos \phi$ in funzione di s, per poter calcolare l'integrale, che avrà per estremi $s=r-R$ e $s=r+R$.

La superficie totale di un guscio sferico è

$4\pi R^{2}$

mentre quella dell'anello tra θ and θ + dθ è

$2\pi R^{2}\sin \theta \,d\theta$

Se $M$ è la massa totale del guscio sferico, quella dell'anello risulta quindi:

$dM={\frac {2\pi R^{2}\sin \theta }{4\pi R^{2}}}M\,d\theta =\textstyle {\frac {1}{2}}M\sin \theta \,d\theta$

Per la legge del coseno (o teorema di Carnot) ed altre semplici considerazioni trigonometriche si ha che

$\cos \phi ={\frac {r^{2}+s^{2}-R^{2}}{2rs}}$

$\cos \theta ={\frac {r^{2}+R^{2}-s^{2}}{2rR}}.$

Differenziando la seconda equazione rispetto a $\theta$ e s si ottiene inoltre che

$\sin \theta \,d\theta ={\frac {s}{rR}}\,ds$

Possiamo quindi esprimere l'integrale rispetto alla variabile s, ed otteniamo

$F={\frac {GMm}{4r^{2}R}}\int _{r-R}^{r+R}\left(1+{\frac {r^{2}-R^{2}}{s^{2}}}\right)ds.$

Il valore dell'integrale è 4R, quindi si ottiene che

$F=G{\frac {Mm}{r^{2}}}$

che è la forza esercitata da una particella di massa M posta a distanza r (ovvero al centro del guscio) dalla particella m, come volevamo dimostrare.

Seconda affermazione

Punto all'interno di un guscio infinitesimo

Suddividiamo il guscio in gusci di spessore infinitesimo dS. Sia P una massa puntiforme all'interno del guscio infinitesimo. Se facciamo passare per P un cono di semiapertura (infinitesima) α il suo asse incontra il guscio nei punti A e B. L'area della superficie del guscio sferico contenuta all'interno del cono dalla parte di A sarà proporzionale al quadrato della distanza PA. Lo stesso dicasi per B. Detta σ la densità, la massa dei due volumetti sarà, rispettivamente

$m_{A}=\sigma \pi \left(PA\,\operatorname {tan} \alpha \right)^{2}\times dS$

$m_{B}=\sigma \pi \left(PB\,\operatorname {tan} \alpha \right)^{2}\times dS$

Se ora calcoliamo la forza gravitazionale esercitata dai due volumetti su P, detta $m_{P}$ la sua massa, abbiamo

$F_{A}=G{\frac {m_{P}\times m_{A}}{PA^{2}}}=Gm_{P}\times \sigma \pi \operatorname {tan} ^{2}\alpha \times dS$

$F_{B}=G{\frac {m_{P}\times m_{B}}{PB^{2}}}=Gm_{P}\times \sigma \pi \operatorname {tan} ^{2}\alpha \times dS$

Dato che le due forze agiscono nella stessa direzione, ma sono di verso opposto, essendo uguali in modulo, si annullano, annullando dunque l'influenza del guscio infinitesimo. Con una semplice operazione, estendendo l'integrale al guscio sferico, si vede che il campo gravitazionale, all'interno del guscio sferico, è nullo.

Potenziale del campo gravitazionale generato da una sfera omogenea

Estendendo il discorso ad una sfera omogenea di centro O, per un punto P situato all'interno, agli effetti del campo gravitazionale, deve considerarsi solo la materia contenuta all'interno della sfera di centro O, e raggio OP. La cosa si vede facilmente considerando la sfera più grande di raggio R come composta da un guscio sferico di spessore R-OP e da una sfera di raggio OP.

Voci correlate

• Gravità
• Teorema del flusso

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file su Teorema del guscio sferico